Sphere Mesh Creation

Generating a sphere mesh is a rather solved problem, but I wanted to go through it myself nevertheless.

The easiest way to get a sphere would be to load up a 3d modeller, create a sphere, export it, and then write a loader for whatever the format was. I wanted to make a sphere mesh generator. It can't be that hard, now can it?

The basic idea is to take a simple object, such as a tetrahedron, cube, octahedron, dodecaedron or some such, and then divide the surfaces. After division, we "push" all the vertices in the direction of their normals (out of the center of the object) so that they're all the same distance from the center.

Repeating this process a few times turns any of those simple objects into a sphere. Starting from an octahedron creates fairly same-sized triangles. Octahedron is also a very simple object to create by hand.

In an octahedron, you have six vertices, each of which only have one non-zero component, for example:

static GLfloat vtx[] =
{
	 0.0f, -1.0f,  0.0f,
	 1.0f,  0.0f,  0.0f,
	 0.0f,  0.0f,  1.0f,
	-1.0f,  0.0f,  0.0f,
	 0.0f,  0.0f, -1.0f,
	 0.0f,  1.0f,  0.0f
};

static GLuint idx[] =
{
	0,    1,    2,
	0,    2,    3,
	0,    3,    4,
	0,    4,    1,
	1,    5,    2,
	2,    5,    3,
	3,    5,    4,
	4,    5,    1
};

Six vertices, eight triangle faces, twelve edges. The orders are important for backface culling.

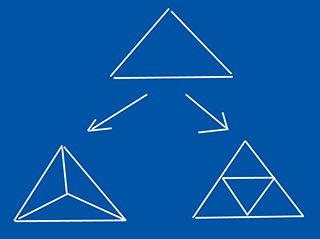
There's principly two ways to split a triangle into several.

One way is to add a vertex in the middle and connect each of the pairs of original vertices to it. The good side of this tesselation is that it's very easy to implement. Bad side is that it's the completely wrong approach in this case. The resulting object will get rounder, but since all the original edges are intact, the result resembles an apple way past its best-before date.

The better way is to split all of the edges. This is somewhat trickier, especially if you don't want to end up with truckloads of duplicate vertices; you have to check if the neighboring triangle already split this edge.

Third way would be to split only one edge at a time, but that would result in really long triangles, and it's not all that much easier than the split-all-edges method.

Fine, the mesh is done. The next problem is how to texture map it. This turned out trickier than it sounded.

Getting a single 2d texture map onto a ball requires spherical uv coordinates, for example like this:

len = sqrt(x * x + y * y + z * z);
u = acos(y / len) / M_PI;
v = (atan2(z, x) / M_PI + 1.0f) * 0.5f;

There's several problems with this approach - after all, 2d textures don't really wrap onto a sphere (just try to wrap a piece of paper neatly on a ball). For instance, there's much higer texture resolution towards the poles, and if you look at the lower tesselation images above, you'll note that there's pieces of the texture map missing.

These are simply limitations of the method. Better solutions exist - using a cubemap is probably the easiest solution - the sphere's normals will double as texture coordinates (generating said map may be more of a headache though), and there's also something called HEALPix to map a specially-formated 2d map neatly onto a sphere.

Anyway, we're doing things the old-fashioned way. This leads to some issues:

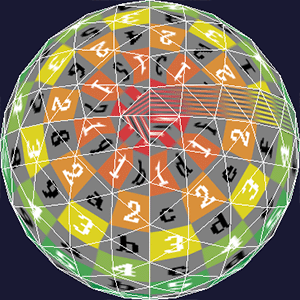
The colorful strip on the right side of this image (which looks at the north pole of the sphere) is due to the fact that on one side of the strip, UV coordinates are 0.0, while the other is closer to 1.0. Thus, the whole texture is drawn "backwards", causing that artifact.

To solve this, we need to duplicate some vertices. To figure out which, I wrote a routine that scans all the triangles, and duplicates a vertex whenever the u coordinate changes more than 0.25 within one edge. The duplicated u coordinate is decremented by 1.0.

As a result the strip goes away (the texture map object itself must be set to wrap for things to work correctly)

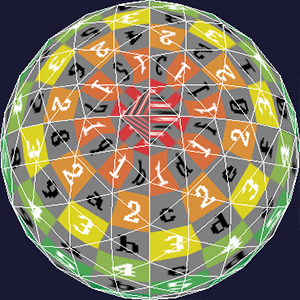
The cap was still buggy. This is due to the fact that there's only one u coordinate for the pole vertex, while the triangles that share said vertex are depending on different u coordinates.

So, I made code that figures which vertices are the pole ones, and then duplicated said vertices as many times as they were shared. The u coordinate was calculated by averaging the u of the other two vertices of each of those triangles.

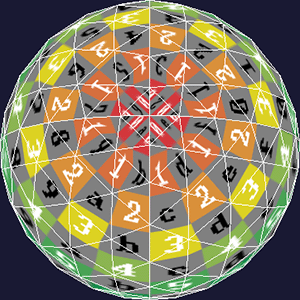
And poof, that bug goes away.

It's still not perfect, as you can see, and the mapping problems get worse the closer you get to the pole. These problems can be reduced by upping the tesselation - the spheres I've used as examples are rather low-poly. It's worth keeping in mind that the problems will never completely go away by tesselating further.

Anyway, now that we have a working solution, let's just slap an earth texture on it and..

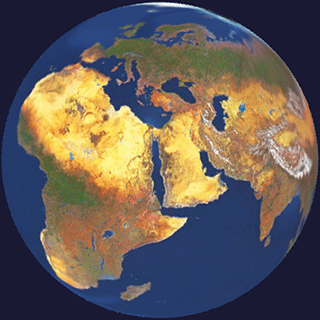
It does occur to me that the ice caps of Earth's poles just might be there to hide UV mapping issues. =)

Further work, apart from using one of those fancier mapping methods, would be to using the fact that we're in control of the mesh generation to make a spherical heightmap. With high enough tesselation, mountains etc. would really stand out.

(As always, comments are appreciated).