Algorithm optimization
Or, 'why clock cycle optimizations don't really matter'
Download the visual C sources(5k) - I don't duplicate the source here.
The binaries(102k) are also available if you don't wish to compile the sources yourself.
In this little tutorial-ish I'm building a simple program to scan through a text file and count the occurrences of every word. (i.e.. how many times word 'the' occurs in the directx5 documentation - 25155). As a test input file I've used ASCII versions of directx5 documentation, ddraw.txt, dmusic.txt and d3dim.txt, total file size being 2176KB.
The program has two pieces; client program (wc.cpp) and the algorithm part (see gen0.cpp for minimal implementation that does nothing). Client program is the same for all generations of the optimization.
The client program performs the following tasks:
- Read through the input file, counting words
- Call the init of this generation (none of the generations do precalculation)
- Get the start tick count
- Parse through the input file, feeding each word separately to the counter code
- Print out a status report once per second
- Get the end tick
- Print status
- Call the generation's report routine, which calls back to the client program's insertion sort routines, and then outputs output.txt.
Yes, the insertion sort I've used is not the fastest possible method for sorting, and could be improved, but it's outside the focus of this document.
So what our to-be-optimized code actually needs to do:
- Keep track of word counts
- Give out all word counts back to the insertion sort
In the first generation I built a very naive implementation; keep a single-linked list of all words, scanning through the list with string compare. The resulting program chowed upon the input file (cpp.txt 2227968 bytes, about 303klines) for about 173 seconds on a p3/600. The obvious bottleneck is, naturally, the string compare.
However, we can be rather confident that the algorithm works. Here's a bit from the result file:
25155 the
7260 to
7019 a
6387 of
5586 is
4633 in
4213 and
4152 for
3438 windows
2922 this
...
Thus, in the second generation I used a checksum for quick comparisation of the strings, but instead of just making a simple sum I created a hash function to calculate almost perfect unique values for the strings (actually, for short strings it is perfect). The result was 121.685 seconds, 2497.876 words per second - about 70% of the original time. Now, through profiling and thinking it's somewhat easy to figure out that the next bottleneck is the tree traversing.
The third generation also stores the hash values and links to the list in a linear buffer, thus eliminating most of the tree traversing. Result of this very simple optimization was staggering - 8.172 seconds, 37194.567 words per second - 5% of the original time, or 7% of the 2nd generation time. That's just about wraps it up for obvious optimizations, though - plus the implementation uses a huge static table for the records which should really be dynamically allocated and resized every time it's getting full (thus slowing it down).
Now let's look at these three generations a bit:


progress bars of generations 1 through 3
While the third generation is obviously faster than the first two ones, it still contains the main problem of the general algorithm. If we scale the progress bars and overlay them, we get the following image..
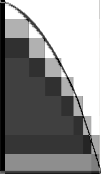

the progress bars, scaled and layered
The point of this image is to show that all of the generations grow slower the more data we have.
The main problem with all of the previous generations was that they have to go through, on average, 50% of the currently stored words to find the old record, or 100% of it on search misses, wasting lots of time. Instead of taking the bottleneck-breaking approach, I tried something a little bit different in the fourth generation: radix search trees (I could have tried hash searches as well, which may or may not have resulted in even better performance).
The radix search tree works this way: start from the root, compare the checksum, if no hit, compare the first characters; if they match, go one way in the tree (child), if they don't match, go the other way (sibling). Eventually you either find the word, or you have a miss, and create a new leaf.
Example:
direct3d
**d**imensional
d**i**rectx
immediate
**i**nterface
i**n**formation
i**n**to
**i**s
mode
application
**a**pi
programming
**p**art
...
So if we were adding 'international' to the above tree, we would go through the following path:
direct3d (sibling)-> immediate (child)-> interface (child)-> information (sibling)-> into (child)-> search miss, create new node as child of into.
The result: 0.931 seconds, 326481.203 words per second - 0.6% of the original, 0.8% of second and 13% of the third generation. And if you enlarge the source file, the gap grows further, as all the earlier generations grow slower much faster the more data you have.
To test if the routine works, I checked the result file, which, while not equal to the ones outputted by the earlier generations, contains the same relevant data, ie. the only differences are in the ordering of items with the same value (ie. the words with just one hit are in different order).
As an interesting addendum, the do-nothing generation takes 0.561 seconds..