Rendering Lots of Cubes
While working on one hobby engine of mine, I came to the realization that I really want to render tons of cubes. What would be the best way of doing so?
Problem definition:
Render lots of cubes with separate transformation matrices for each which may change each frame.
Step 1: Vertex Arrays
As the first step, I wrote an application that would simply render tons of cubes. I did consider making a version that uses glBegin..glEnd, but decided to skip that and used vertex arrays as the starting point. Which was nice, as vertex arrays can be rather easily converted to VBOs down the line.
Once I got some cubes rendered, I incresed their number until the application was sufficiently slow to start optimizing. On my system, rendering 125000 cubes ended up taking about 193ms. This is what it looks like:
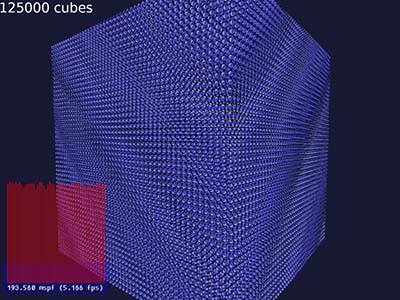

The uniform grid of 50 by 50 by 50 cubes might not be the most fun to watch, but at least it would tell me rather quickly if I messed something up.
So, here's the starting point:
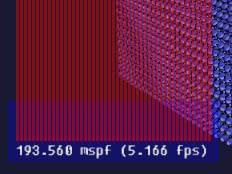

Pros: Works with any OpenGL version.
Cons: Slow.
Step 2: Vertex Buffer Objects
The obvious optimization is to use VBOs instead of arrays. These are currently supported basically everywhere, even including the intel chipsets on netbooks.
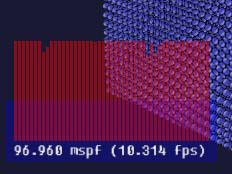

Pros: Works almost anywhere, easy to fall back to arrays if needed.
Cons: None.
Step 3: Configurable Math Library
Next step, since we're eventually going to use shaders, was to replace the OpenGL's fixed function matrix math with an external library. I like CML, or configurable math library. It's not perfect (what is?), but it's the most comfortable library I've found so far. It's basically all c++ templates, but compiles into rather fast code, as can be seen from the result:
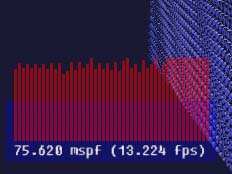

Pros: Works anywhere, more flexible than OpenGL's built-in math stuff.
Cons: Requires C++, debug builds rather slow.
Step 4: Shaders
I wrote minimal shaders - vertex shader just transforms the incoming vertex with the gl_ModelViewProjection matrix, and the fragment shader just grabs a single texel and outputs it. Much to my surprise, this was slower than fixed function pipeline, even though it should do much less work. The variance in per-frame timings that can be seen in the graph are due to mouse movements.
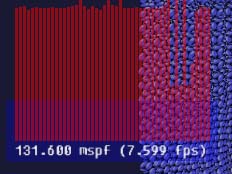

Pros: Flexibility.
Cons: Doesn't work on lots of old hardware and not even on most of the new intel hardware.
Step 5: Pseudoinstancing
Next easy step was to implement pseudoinstancing (warning: pdf link). Basically what this means is that we abuse the fixed-pipeline variables, texture coordinates to be precise, to send the matrix to the shader. Note that we're still drawing one cube at a time!
From the application's point of view, this means doing:
glMultiTexCoord4fv(GL_TEXTURE1, (float*)active_matrix.data());
glMultiTexCoord4fv(GL_TEXTURE2, (float*)active_matrix.data()+4);
glMultiTexCoord4fv(GL_TEXTURE3, (float*)active_matrix.data()+8);
glMultiTexCoord4fv(GL_TEXTURE4, (float*)active_matrix.data()+12);
And on the shader, we grab these to build a matrix by:
mat4 mvp = mat4(gl_MultiTexCoord1,
gl_MultiTexCoord2,
gl_MultiTexCoord3,
gl_MultiTexCoord4);
This is faster than using glLoadMatrix or using a matrix uniform. This makes little sense to me, as the amount of data is the same. Sounds like there's still plenty of fixed-function helpers in the hardware..
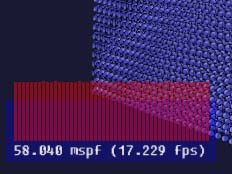

Pros: Easy to implement, clear performance gain at least on some Nvidia hardware. (Yes, I tried with ATI, it's SLOW).
Cons: Limited amount of data, as there's limits to the texcoords we can abuse.
Step 6: The ARB_draw_instanced extension
One of two extensions in OpenGL regarding instancing (e.g. drawing the same geometry bazillion times) is called ARB_draw_instanced.
Basically what this extension does is introduce a new draw call, which adds a parameter on how many times the object should be rendered. Since this has rather limited usability, it also adds a variable to the shaders telling which instance we're rendering, and the shader can make its own conclusions based on that.
The trick here is how to get the correct matrix to the correct instance. My first attempt was to use an uniform array, which unfortunately has a rather limited size. Hence, I could only render about 200 instances at once - and most likely much fewer on less-capable hardware (the ATI card I have, while similar in power with my nvidia card, has smaller uniform storage). The results were rather underwhelming (but don't stop reading):
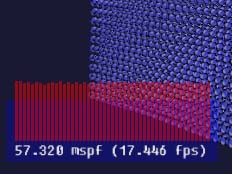

Pros: Reduced API overhead.
Cons: Further limits the target market to about 2-3 latest generations of Nvidia and ATI hardware. Check the database in OpenGL extensions viewer to see the supported hardware.
Step 7: Precalculated Matrices
There's several possible bottlenecks here. First was the API overhead - calling draw on every single cube; that could be handled with the draw_instanced extension. Second is the fact that I was still calculating those matrices on every frame, which was overkill left over from using OpenGL's internal matrix math. The third was the fact that the matrices were copied to the video hardware each frame. (125000 * sizeof(float) * 4 * 4 = about 8 megs).
If you remember the problem statement, it said the matrices may change every frame. It doesn't say they must.
So, by precalculating the matrices to an array and just using those copies instead, we arrive at:
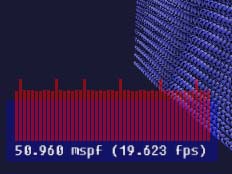

Pros: n/a.
Cons: n/a.
Step 8: Matrices in a Texture
Now the most obvious optimization is to keep the data on the video card. Unfortunately, the uniform array was way too small to store all of the matrices, so I had to move them over to a texture.
There's a few tricky bits in this. First is the exact way to create a texture.
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA32F, 1024, 1024, 0, GL_RGBA, GL_FLOAT, texdata);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
Alternatively GL_TEXTURE_RECTANGLE could be used as target, which may simplify calculations on the shader side.
Yes, I know, a smaller texture would have been sufficient.
Next bit is the shader side, which for my quick test turned out as:
int y = (gl_InstanceID * 4) / 1024;
mat4 mvp = mat4(texture2D(vtxtex, vec2((gl_InstanceID * 4 + 0) & 1023, y) * (1.0 / 1024.0)),
texture2D(vtxtex, vec2((gl_InstanceID * 4 + 1) & 1023, y) * (1.0 / 1024.0)),
texture2D(vtxtex, vec2((gl_InstanceID * 4 + 2) & 1023, y) * (1.0 / 1024.0)),
texture2D(vtxtex, vec2((gl_InstanceID * 4 + 3) & 1023, y) * (1.0 / 1024.0)));
Note that I did not test the above on ATI hardware yet, it probably won't compile due to missing typecast (int to float) at least. Nvidia is a bit too lax on syntax, but at least it lets me test things out quickly.
The result was slightly better than I actually expected:
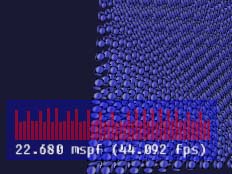

Pros: The resuls pretty much speak for themselves.
Cons: Texture fetch from vertex shader requires high-end hardware, but on the other hand, the extensions in use do so anyway.. Also, more complex geometry will make this approach slower too =(.
Other Ideas
There's another extension, called ARB_instanced_arrays which may or may not be more suitable in this case. At least it should be possible to ditch the texture fetch and use vertex attributes instead. Unfortunately, even though Nvidia tends to be extension-crazy, they haven't implemented this extension yet.
Note that this did not include any of the "obvious" optimizations like visibility culling or baking static geometry into larger (and fewer) objects.
Since this was just a quick hackish research thingy, I'm not posting source at this time. In fact, the resulting project breaks lots of rules, the shaders generate plenty of warnings (using features from GLSL 1.4 but also those deprecated in GLSL 1.2), and so on. Still, I can use the results from this research for future projects.
Now that nvidia has finally the instanced_arrays extension, I ran a test with it. The results were more or less identical with the matrix-in-texture case, but much cleaner, API-wise.
So.. baked geometry is (still) the way to go. Bummer.
Benchmarking a Bit
I went back and did some more scientific(tm) benchmarking of different methods. The two computers I used are otherwise identical, except that one has nvidia gtx260 and the other has ati hd5700 video card. In both machines, sync to refresh was disabled, and I removed all sleeps and yields from the test application.
The test setup uses 64000 instances, and the geometry includes cubes in vertex arrays or not, and low (80 tris) and high (230 tris) poly count toruses. I did not run through all test cases on both machines, because some of these tests take a long time to run.
Specifically non-vbo instanced arrays were extremely slow on nvidia, and my matrices in uniforms case doesn't run on the ati board even though I'm "only" using an array of 32 matrices (the nvidia board can do 100).
| Nvidia | ATI | |||||||
|---|---|---|---|---|---|---|---|---|
| Cubes(VA) | Cubes(VBO) | Torus(lo) | Torus(hi) | Cubes(VA) | Cubes(VBO) | Torus(lo) | Torus(hi) | |
| No shaders | 59.3ms | 41.1ms | 41.1ms | 55.3ms | 49.2ms | |||
| Plain shaders | 86.7ms | 80.5ms | 81.0ms | 80.4ms | 50.0ms | |||
| Pseudoinstancing | 70.1ms | 30.0ms | 30.4ms | 51.9ms | 103.6ms | |||
| Matrices in texture | 41.0ms | 10.4ms | 22.8ms | 50.7ms | 18.8ms | 2.8ms | 12.2ms | 23.0ms |
| Matrices in uniforms | 45.5ms | 18.7ms | 23.1ms | 50.5ms | ||||
| Instanced arrays | 11.3ms | 22.8ms | 53.2ms | 19.3ms | 2.8ms | 12.2ms | 23.0ms |
Nevertheless, the two most interesting cases are the matrices-in-texture and instanced arrays, and surprisingly enough the texture case seems to win by a slight margin. The instanced arrays extension is, however, so much cleaner way to do things that I would not bother with the texture matrix hack for such slim gains.
It's also worth noting that the pseudoinstancing hack is so slow on ATI that one shouldn't consider it for a moment.
Comments, etc, appreciated.